Describe in Your Own Words the Central Limit Theorem

The central limit theorem allows us to use a normal distribution for some very meaningful and important applications. Central limit theorem is a statistical theory which states that when the large sample size has a finite variance the samples will be normally distributed and the mean of samples will be approximately equal to the mean of the whole population.

Central Limit Theorem Overview History And Example

Before selling it a researcher wants to test its effectiveness.

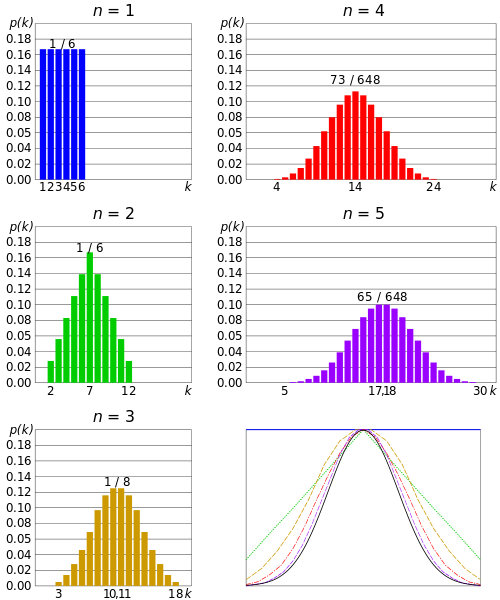
. The population mean for a six-sided die is 1234566 35 and the population standard deviation is 1708. Now hit the 5 times button to do 5 samples at a time. It allows us to understand the behavior of estimates across repeated sampling and thereby conclude if a result from a given sample can be declared to be statistically significant that is different from some null hypothesized value.

The central limit theorem is perhaps the most fundamental result in all of statistics. We may ask about the overall shape of the sampling distribution. In simple terms the theorem states that.

The central limit theorem also states that the. μ x μ. The Central Limit Theorem which is widely regarded as the crown jewel of probability and statistics is the most beautiful and important theorem in probability theory.

Keep hitting the 1 time button many times and look at the shape of the distribution that falls out. In other words the central limit theorem states that for any population with mean and standard deviation the distribution of the sample. What is the central limit theorem Please describe it in your own words.

The central limit theorem CLT states that the distribution of sample means approximates a normal distribution as the sample size gets larger regardless of the populations distribution. Before we go in detail on CLT lets define some terms that will make it easier to comprehend the idea behind CLT. σ x σ n.

The theorem states that if we add identically. Where μ Population mean. The central limit theorem CLT states that the means of random samples drawn from any distribution with mean m and variance s2 will have an approximately normal distribution with a mean equal to m and a variance equal to s2 n.

An educational enrichment company wants to sell an at home learning module for children that is intended to improve their scholastic ability. σ Population standard deviation. For example college students in US is a population that includes all of the college students in US.

Visit BYJUS The Learning App to know the central limit. The central limit theorem says that this sampling distribution is approximately normalcommonly known as a bell curve. You will see 5 random data points are chosen and the mean and standard deviation of that sample are shown.

The formula for central limit theorem can be stated as follows. Thus if the theorem holds true the mean of the thirty averages should be. The central limit theorem clt for short is one of the most powerful and useful ideas in all of statistics.

Unpacking the meaning from that complex definition can be difficult. The law of large numbers says that if you take samples of larger and larger size from any population then the mean of the sampling distribution μ x. The central limit theorem states that for a large enough n X-bar can be approximated by a normal distribution with mean µ and standard deviation σ n.

Saul McLeod published Nov 25 2019 The central limit theorem states that the sampling distribution of the mean approaches a normal distribution as the sample size increases. Generate a sample distribution of n 5 and hit the 1 time button. The meaning of CENTRAL LIMIT THEOREM is any of several fundamental theorems of probability and statistics that state the conditions under which the distribution of a sum of independent random variables is approximated by the normal distribution.

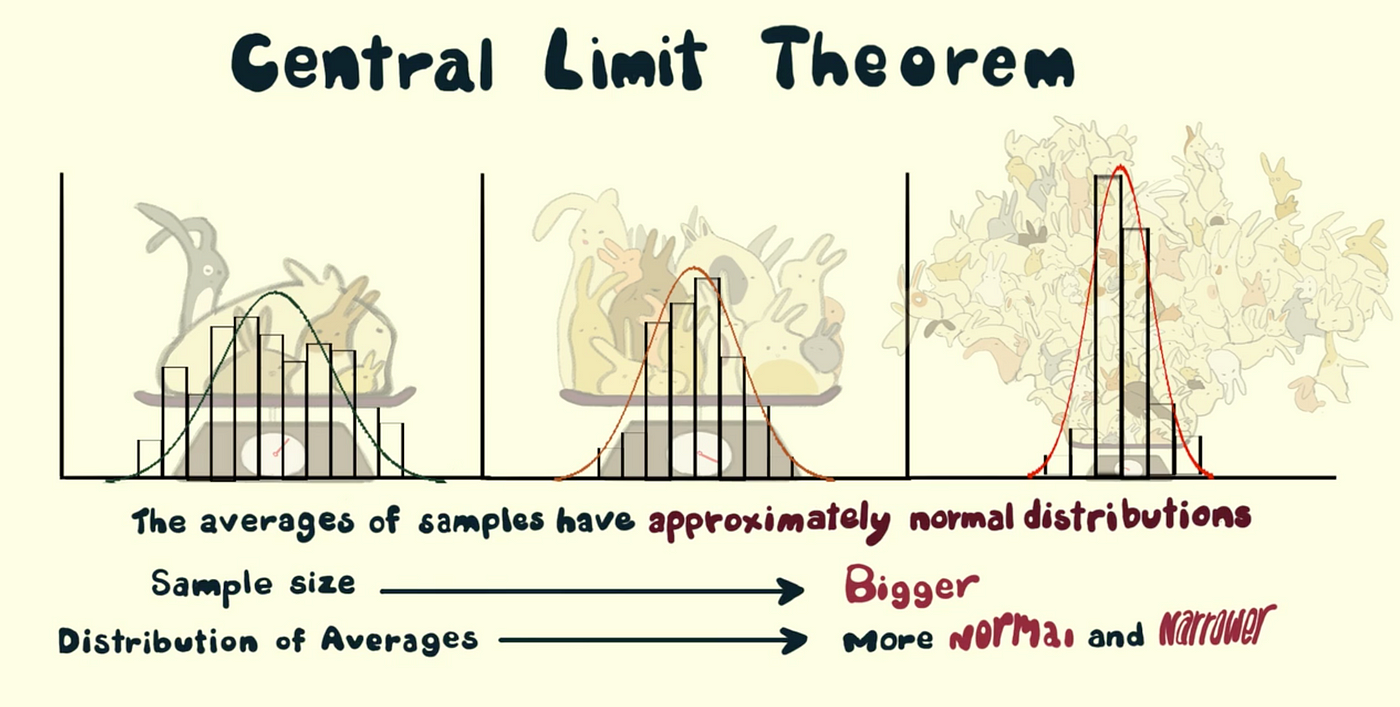
This approximation improves as we increase the size of the simple random samples that are used. Why is it so important to statistics. The Central Limit Theorem CLT is a statistical concept that states that the sample mean distribution of a random variable will assume a near-normal or normal distribution if the sample size is large enough.

Thats the topic for this post. For those new to statistics this definition may seem a bit intimidating. Central limit theorem is applicable for a sufficiently large sample sizes n 30.

The central limit theorem CLT is a fundamental and widely used theorem in the field of statistics. The central limit theorem concerns the sampling distribution of the sample means. The central limit theorem states that the sampling distribution of a sample mean is approximately normal if the sample size is large enough even if the population distribution is not normal.

What is central limit theorem in statistics. There are two alternative forms of the theorem and both alternatives are concerned with drawing finite samples size n from a population with a. One which is much applied in sampling and which states that the distribution of a mean of a sample from a.

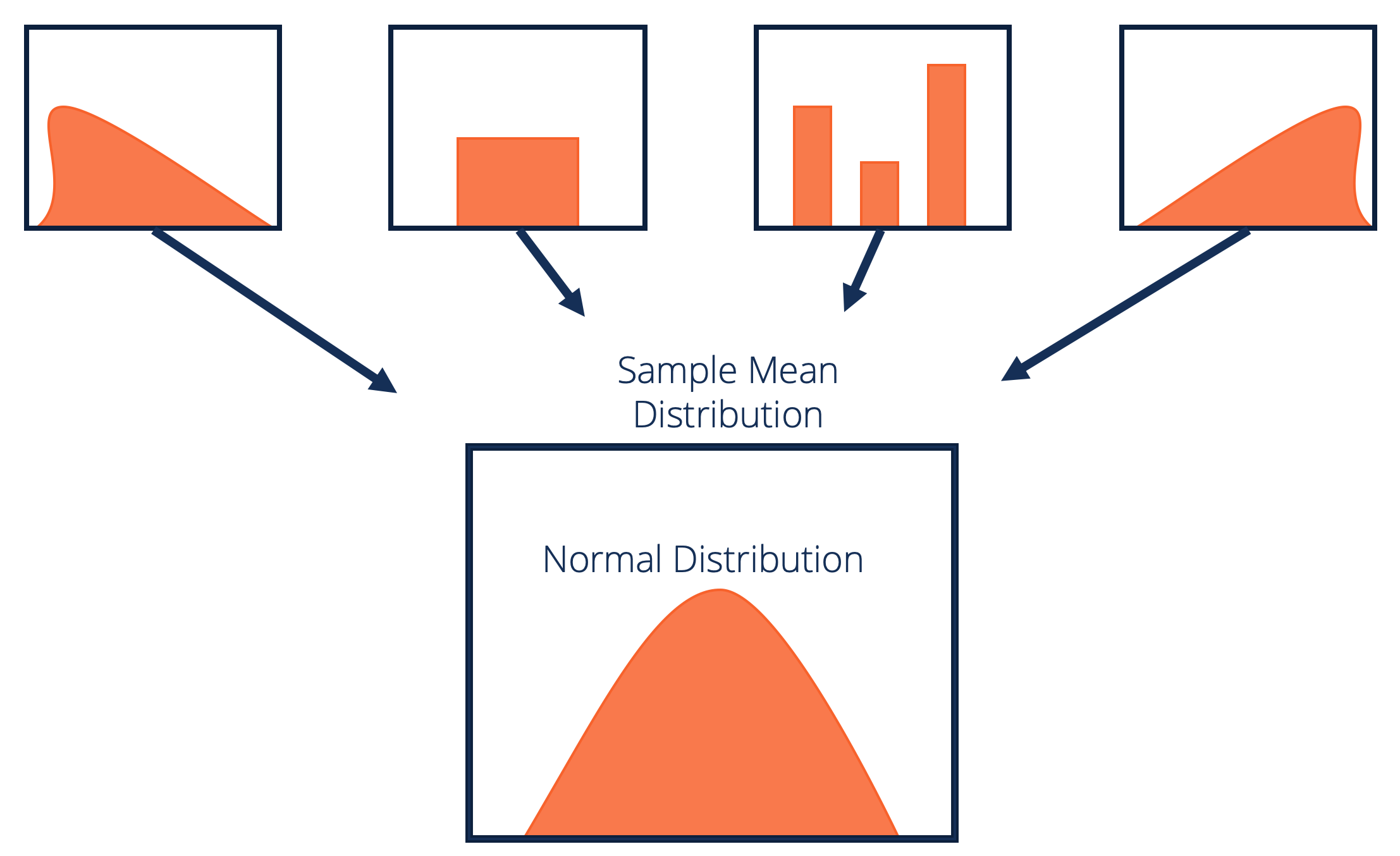
What Is The Central Limit Theorem Try To State It In Your Own Words. The Central limit theorem explains that the mean of all the given samples of a population is the same as the mean of the population approx if the sample size is sufficiently large enough with a finite variation. From the Central Limit Theorem we know that as n gets larger and larger the sample means follow a normal distribution.

The theorem states that if we add identically distributed independent random variables then their normalized sum will tend towards a normal distribution. The central limit theorem also tells us that no matter what the distribution of the population is the shape of the sampling distribution will approach normality as the sample size N increases. The central limit theorem in statistics states that given a sufficiently large sample size the sampling distribution of the mean for a variable will approximate a normal distribution regardless of that variables distribution in the population.

Population is all elements in a group. The researcher obtains a. μ x tends to get closer and closer to the true population mean μ.

Central Limit Theorem Definition And Examples Statistics How To